本文共 677 字,大约阅读时间需要 2 分钟。
| 1路万兆光纤SFP+和1路千兆网络 FMC子卡模块 |
| 
一、概述 该板卡是基于kc705和ml605的fmc 10g万兆光纤扩展板设计,提供了1路万兆光纤SFP+和1路千兆网络接口。可搭配我公司开发的FPGA载卡使用。载卡可参考:ID=204 SFP+(10 Gigabit Small Form Factor Pluggable)是一种可热插拔的,独立于通信协议的光学收发器,通常传输光的波长是 850nm, 1310nm 或1550nm,用于10G bps的SONET/SDH,光纤通道,gigabit Ethernet,10 gigabit Ethernet和其他应用中,也包括 DWDM 链路。SFP+包含类似于 SFF-8472 的数字诊断模块,但是进行了扩展,提供了强大的诊断工具。 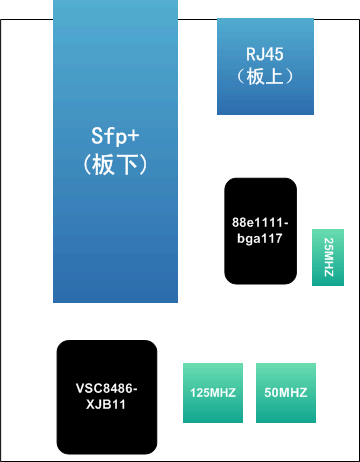
二、性能指标 板卡提供一路phy(VSC8486-XJB11)和一路phy(88e111)芯片。 2.1 接口卡标准采用1路10g以太的phy和1路千兆的phy88e1111 2.2 Fpga端口1路ip使用xaui,另1路ip使用rgmii 2.3 万兆时钟由fmc板卡提供156.25MHZ时钟给主板 2.4 千兆时钟由fmc板卡提供 125MH和25MHZ和备用时钟50MHZ三、物理特性 储存温度:-20℃~ +70℃ 存储温度:商业级0℃~ +55℃ ,工业级 -20℃~ +55℃ 工作湿度:10%~80%四、软件支持 4.1 基于204号板卡的GE接口测试代码; 4.2 光纤接口测试代码 4.3 基于204号板卡的的ibeart自发自收验证; | |
转载地址:http://iynlz.baihongyu.com/